Introduction | What is DinosaurTheory? | Square-Cube Law | Dinosaur Paradox | Science of Flight
Search for the Solution | Thick Atmosphere Solution | Biology Revolution | Earth's Heat | Solar System
Blue Planet | Rocks and Fossils | Dinosaurs and Dragonflies | For the Birds | Planetary Evolution
About Author | Scientific Theories | Educational Resources | Home Page | Contact
DinosaurTheory Store

© DinosaurTheory.com. All rights reserved.

Flying Ability of Various Planes and Animals

Flyer	Weight (N)	Front Area Estimate (m2)	Drag Coefficient Estimate (Front Area)	Wingspan (m)	Speed for least Power (m/s)	Minimum Power (kW)	Available Power (kW)	Power Ratio
Cessna 172	10900	4.0	0.17	11	28	37	84	2.3
Sopwith Camel	6500	2.8	0.50	8.5	21	30	68	2.3
Wright Flyer	3340	1.7	0.50	12.3	14	5.7	6.3	1.1
Spruce Goose	2300000	110	0.17	97.5	60	9900	13000	1.3
Human Flight	980-610	1.7	0.12	23.2	7.8	0.24	0.29	1.2
Starling	0.74	0.0080	0.20	0.36	5.8	0.00077	0.0051	6.6
Giant Bat	11.8	0.070	0.50	1.5	5.2	0.013	0.021	1.6
Condor	102	0.19	0.20	2.9	11	0.12	0.13	1.1
Argentavis	1400	1.1	0.20	7	17	2.5	0.77	0.3
Quetzalcoatlus	7000	2.5	0.50	12	18	20	1.8	0.09

Calculated Valued	The Equations	Inserting the Values
Speed for least Power (m/s)
Power Required for Flight (W)
Power Available -Plane (W)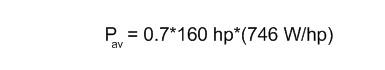
Power Available -Bird (W)

In the first three rows of the table above the data for the Cessna 172 is used as an example to show how the the speed for least power, power required for flight, and the available power were calculated. In the last row the Starling data is used to give an example of how the available animal power was calculated.

Discussion of the Table

The power flight equation applies to just about anything that we might have a reasonable belief of it being able to fly. As stated earlier, fulfilling the power requirement does not guarantee that something will fly, but rather it says that not fulfilling the power requirement guarantees that it will not fly. Beyond supplying a plane with sufficient power aerodynamic engineers must fulfill numerous other criteria such as wing shape, flight control, center of mass and so on to assure that a plane will fly. Likewise the process of evolution favors species to evolve in the direction of a favorable form that is best suited for flight.

Notice the wide variety of flyers listed. Some are planes, some are flying animals; human flight is both a plane and a flying animal. Some like the starling is small and lightweight while at the other extreme the loaded Spruce Goose is a couple hundred tons. Most of the chosen flyers are slow to moderate speed flyers but the power for flight equation works for transonic and supersonic aircraft as well. The power for flight equation is general meaning that for the most part if something has wings then the equation is applicable. The reader is encouraged to explore the utility and versatility of the flight power equation by looking up the specifications for planes and calculating their power ratios.

Moving to the second column heading, weight is arguable one of the most important criteria in determining minimum power requirements. Most of the weights come directly from reliable references for either the planes or the birds. The weights that require further explanation, the Spruce Goose, human flight, the Argentavis, and the Quetzalcoatlus are given in the summary comments of each flyer.

Because most plane specifications do not give front area and to the author’s knowledge this information is not record for birds, most of the Front Areas are estimates. Starting with the best guess of 3.0 m² value for the Cessna 172 the other values were initially scaled proportionally from this value. Then some additional tweaking was done according to known differences of the shapes of the flyers. The drag coefficient values were generated in a similar fashion; first starting with actual data for the Cessna 172 and then making judgments regarding the other values based on difference of the shapes of the flyers. Obviously the author’s preference would be to use reference data instead of relying on partial calculations partial best judgment in generating these values, but for many of these flyers this data simply does not exist. Fortunately while front area and drag coefficient data are important, these two values are not nearly as critical as weight and wingspan in determining power requirements.

Regarding the aerodynamic drag coefficient C, physics and the aviation industry use different areas for calculating this value and thus creating the potential for confusion. Because the amount of drag is a function of the front-facing or greatest cross-sectional area, from a science perspective it is logical to calculate the drag coefficient value based on the front facing area. However a drag coefficient calculated by using the wing area produces a smaller numerical value and this may please a potential buyer who is unaware that a larger area is being used in the calculation. The equation C_F = C_W (A_W / A_F) is useful in converting from the aviation industry’s drag coefficient to the physics drag coefficient that is used here.

The wingspan, not the wing area, is the key variable in determining lift.

Speed for least power can be thought of as the takeoff speed. Actually a plane should reach a speed of at least 20% greater than this before putting the plane into a climb. The extra speed is an insurance against a strong gust of wind or some other mishap stalling the wings during the takeoff.

The minimum power speed and the other necessary variables are inserting into the power equation to compute the theoretical minimum power needed for flight. This value does not consider ground effect or any additional power a flying object may receive from rising air thermals.

The available power for the planes is calculated by multiplying the engine power by 0.70. Because of engine and transmission friction and because the propeller is unable to transfer all the energy to the air, only about 70% of the power from the engine is effectively in thrusting the plane forward. For human flight a 0.80 factor is used rather than 0.70 to account for the slightly greater efficiency. The available animal power is calculated based on the weight of the animal. The equation used for this calculation P³ = (69 W³/N²) W² was discussed in the earlier section on the largest flying mammals. The calculate power for mammals is then multiplied by 1.5 to account for the high metabolism / greater power that birds have compared to mammals.

The power ratio not only tells us if something can fly, it tells us how strong of a flyer it is. A flyer with a power ratio of two or above is a strong flyer capable of flying in foul weather. A flyer with a power ratio between one and two is a marginal flyer that is unable to fly in foul weather. A proposed flyer with a power ratio below one is not going to fly.