| Previous Chapter | Return to Home Page | Next Chapter |

2. The Paradox of Large Dinosaurs and Flying Pterosaurs

Applying Science to Understanding Large Dinosaurs

Comparing the Size of a Brachiosaurus to an Elephant

When we go back in time to the Mesozoic Era, the world of dinosaurs seems almost magical, as if the laws of physics no longer applied, allowing them to grow to gigantic sizes.

The discovery of fossilized bones providing evidence of monstrous terrestrial vertebrates has puzzled the scientific community. In all likelihood, if dinosaur fossils had never been found, scientists would have long ago:

Emphasized Galileo’s Square-Cube Law in science education, highlighting the constraints of size, and
Concluded that today’s largest terrestrial animals are already approaching the limits of feasible size.

The brightest scientists strongly believe in a rational reality, and they become intrigued when evidence appears contradictory. Their curiosity about anomalies often leads to major discoveries. One might say that the first step on the road to a Nobel Prize in science begins with the statement, "That’s odd."

The extraordinary size of Mesozoic terrestrial animals is not a minor inconsistency to be dismissed — it is a glaring paradox that demands investigation. At stake is the very foundation of science: our belief in a rational, comprehensible universe.

Something about the world must have been different during the Mesozoic Era to allow terrestrial animals to reach such sizes. This reasoning naturally leads us to ask whether there is other evidence suggesting that Earth was dramatically different during this time. Without getting too far ahead, the author will address this curiosity by stating that, yes, multiple lines of evidence indicate that the Mesozoic world was vastly different from today. The gigantic dinosaurs and pterosaurs are just one of several pieces of evidence pointing to a profoundly different Earth.

The focus of this chapter is to explain the physical limitations that restrict the size of today's terrestrial animals, thereby clarifying why the gigantic animals of the Mesozoic Era present a scientific paradox. Below is a list of specific issues this chapter will address. The first three highlight the evidence demonstrating the anomaly of dinosaurs reaching such large sizes. The final issue, concerning the flight of pterosaurs, will be discussed in the next chapter, as the paradox of their ability to fly becomes fully apparent only after a discussion of the science of flight.

There are four key problem areas illustrating why the largest dinosaurs and pterosaurs present a paradox to science:

Inadequate bone strength to support the largest dinosaurs
Inadequate muscle strength to lift and move the largest dinosaurs
Excessively high blood pressure and heart stress in the tallest dinosaurs
Flight physics showing that the pterosaurs should not have flown

Before addressing the first issue, it is necessary to examine the estimated masses of various dinosaurs. In particular, having accurate mass estimates for the largest dinosaurs, the sauropods, would be especially useful.

How much does your dinosaur weigh?

Skeleton of Brachiosaurus, Chicago Field Museum of Natural History

The most obvious observation about dinosaurs is that they were incredibly large animals. Kids want to know how the dinosaurs grew so large. Yet, oddly enough, many paleontologists would rather avoid this subject. While paleontologists benefit from the public’s fascination with the immense size of these dinosaurs, these same paleontologists find it extremely problematic to provide a scientifically feasible explanation of how the larger dinosaurs could have supported their own weight.

Nearly a century ago, paleontologists thought they had the answer when they imagined that the large sauropods were like hippos in that they spent their days standing in the deep water of a lake or river to support their weight. However, the bone structure of the feet showed that these were truly terrestrial animals, and so the paleontologists wisely discarded this hypothesis. This left the paleontologists back at square one, and in all the time since, they have failed to come up with a reasonable explanation of how these animals grew so large.

Unable to solve the paradox, paleontologists began lowering their mass estimates for the sauropods as their new strategy to make the problem go away. While the first mass estimates for sauropods were around 100 tons or more, ever since paleontologists removed the large dinosaurs from the water, the mass estimates for these dinosaurs have steadily dropped. Most recently, some paleontologists have made the outrageous claim that the Brachiosaurus had a mass of only 23 tons.

back vertebra of Patagotitan mayorum, a Titanosauria that is currently considered to be the larger dinosaur
ever found.

A back vertebra of Patagotitan mayorum, the largest known dinosaur. Its full skeletal mount is the centerpiece of museums in New York, Chicago, and Trelew, Argentina, near its discovery site.

This is unacceptable. Since the paleontology community has taken the position that there is no paradox regarding the dinosaurs' size, there is an obvious conflict of interest. These paleontologists have strained their credibility as scientists by asking the public to believe their low mass estimates.

It may be helpful to learn what is involved in making an estimate of a dinosaur’s mass. To determine the mass of a dinosaur, we just need to know its volume and its overall density, since multiplying the volume and density together gives us the mass. Let us start with determining the volume.

Paleontologists have already completed the work of determining the volume of various dinosaurs. Using dinosaur skeleton displays as references, paleontologists have filled out the form of these animals. They usually work off of computer-generated images or full-size replicas to determine the volume. But it is also possible to work off of authenticated scale models of the dinosaurs created by paleontologists. One of the first and most popular lines of scale dinosaur models is the Carnegie Collection. Paleontologists use the fossil dinosaur displays at the Carnegie Museum of Natural History as their reference in creating these authenticated dinosaur models.

If we know the volume of an authenticated model of a dinosaur and we know how this scales to a full-size dinosaur, then we know the volume of the actual dinosaur. One way of determining the volume of the model is to collect and measure the runoff water created in the process of submerging the dinosaur model in a full tub of water. While this method is intuitive and shows us that the volume of the runoff water is equal to the volume of the dinosaur model, there is another method using Archimedes’ Principle that is more precise and easier to do. With this second method, the weight of the dinosaur model is recorded as it hangs from a scale. Its weight is then recorded again as it hangs from the scale while submerged in the water. The difference between the two readings gives us the weight of the water displaced. Since we know the density of water, the weight of the displaced water gives us the volume of our dinosaur model.

Most of the Carnegie dinosaur models use a one-to-forty scale. This means that if the scale model is one foot long, then the actual dinosaur is forty feet long. Because volume is a function of the scaling multiplier cubed (V = L³), the volume scaling for the model is one-to-forty cubed, or one-to-64,000. If you have an authenticated dinosaur model other than Carnegie’s, and your scale model uses a different scaling ratio, you can still determine your volume scaling ratio by cubing the linear scaling ratio.

Vertebrae from the back of a juvenile Diplodocus preserved in sandstone, Jurassic Period, Trail through Time, Rabbit Valley, 26 miles west of Grand Junction, Colorado

Now that we have determined the volume of our dinosaur, we will move on to calculating its overall density.

Our first step in estimating the density of dinosaurs is recognizing that they were vertebrates and thus shared many characteristics with present-day vertebrates. Modern vertebrates include mammals, reptiles, amphibians, fish, and turtles. There are only slight differences in the proportions of bones, muscle mass, blood, and internal organs among these animals, meaning there cannot be much variation in the density of these components. Most of these components have a density slightly greater than that of water. This should not be surprising, as the human body — and the bodies of most vertebrates — consists primarily of water.

Since the body parts of vertebrates have a density greater than water, we, along with other vertebrates, should sink. However, most vertebrates are neutrally buoyant instead of sinking. This buoyancy is due to the air trapped in the lungs, which provides an upward force that counteracts the downward pull of denser bones and muscle mass. Additionally, because lungs are located in the upper part of the body, most vertebrates tend to float top-side up, making it relatively easy to lift their heads above water for a breath of air. Like us, most terrestrial vertebrates with lungs have an overall body density just slightly less than that of water, meaning they barely float, with most of their body submerged.

However, not all vertebrates rely on lungs for neutral buoyancy. For fish, maintaining neutral buoyancy is an obvious advantage, yet they do not have lungs filled with air to lift them up. Without lungs, some species — such as sharks — must constantly swim to avoid sinking. The sideways pectoral fins of a shark function like wings, generating lift as the shark moves through the water. While this method works for sharks, most fish have evolved an internal air-filled organ known as a swim bladder, which provides the necessary buoyancy to keep them neutrally buoyant. Thus, like terrestrial vertebrates, fish also have a body density very close to that of water.

In terms of body density, birds are the exception. Unlike other vertebrates, birds possess a unique circulating respiratory system that requires a much larger internal cavity, resulting in a lower body density.

Mallard Ducks – Ducks and other waterfowl float high on the water because they have a much lower density than other vertebrates. This lower density is due to their unique respiratory system, which stores air in sacs within their bodies, allowing air to move through their lungs at a steady rate.

Birds’ respiratory system allows fresh, high-oxygen air to move continuously through the lungs. This is achieved as incoming air first fills the abdominal and posterior thoracic air sacs before passing through the lungs to the anterior thoracic air sacs, from which it is then expelled. This superior respiratory system provides birds with the increased oxygen supply, higher metabolism, and greater power necessary for flight.

Waterfowl take this adaptation to the extreme by having an internal cavity volume much larger than what is required for a circulating respiratory system. Their large internal air-filled spaces significantly reduce their body density, enabling ducks, geese, seabirds, and other waterfowl to float high on the water.

Paleontologists claim that birds evolved from Cretaceous theropod dinosaurs. If this were true and if these theropod dinosaurs had developed the unique respiratory system seen in birds before birds themselves evolved, it could create confusion about whether certain dinosaurs had exceptionally low body densities similar to birds. However, the evidence overwhelmingly indicates that birds evolved before these theropod dinosaurs. Furthermore, the earliest birds did not need — nor did they evolve — their specialized respiratory system until after they had already developed the ability to fly.

Thus, we can conclude that the respiratory system of all non-avian dinosaurs was most likely similar to that of present-day non-bird vertebrates. Likewise, their body density was probably comparable to that of modern non-avian vertebrates, which is at or near the density of water (1.0 g/cm³).

Picture of Ornithischia and Saurischia hips, Models of T-Rex and Triceratops

The left side shows the Ornithischians hip while the right side shows the Saurischians hip. Ornithischians and Saurischians are the two main dinosaur classifying groups and this distinction is primarily based on the three bones that make up the pelvis: ilium (green), ischium (red), and pubis (blue). Despite the fact that birds have a hip similar to the Ornithischian dinosaurs many paleontologists are claiming that birds evolved from the Saurischians dinosaurs.

Dinosaur Weighing Kit

We now have everything needed to calculate the masses of various dinosaur species:

M = V ρ ( S.F.)³

where M is the unknown mass, V is the volume of water displaced, ρ is the overall density of the animal, and S.F. is the scaling factor.

The author has clarified the scientific procedure for determining dinosaur masses. While not perfect, making this process transparent allows for greater accountability in obtaining accurate estimates. Scientists can and should continue debating the shapes of various dinosaurs, as even slight changes in shape significantly impact mass estimates. Here is a link that explains the procedure of using authenticated models for determining the mass of dinosaurs.

Using the described procedure the author has calculated the masses for a few well known dinosaurs and has given the results in the table below.

The Mass of Dinosaurs

Dinosaur	Authoritative Mass Estimates (tons)	Mass Determined by Authenticated Dinosaur Models (tons)
Ankylosaurus	4 - 8	6
Triceratops	6 - 12	9
T-Rex	6 - 14	10
Brachiosaurus	23 - 88	88

Results are for the dinosaur models that are shown. Other authenticated dinosaur models may produce slightly different results.

The largest terrestrial animal today is the African elephant, weighing between four and seven tons. The woolly mammoth, which went extinct only 4,000 years ago, was another massive land animal, weighing around six tons. In terms of mass, the six-ton Ankylosaurus fits within this range, making it relatively unremarkable compared to modern megafauna. Even the nine-ton Triceratops is exceptionally large but might still be considered an outlier. However, Tyrannosaurus rex raises more questions—not only was it heavier, but its weight was supported on just two legs rather than four. Once we reach the largest dinosaurs — the sauropods — any hope of reconciling these size differences with modern land animals disappears entirely.

In the past few decades, paleontologists have discovered even larger sauropods than Brachiosaurus, now classified as "super sauropods." Among them are Argentinosaurus and Patagotitan mayorum, both members of the titanosaur group, which includes the largest land animals ever to exist. These dinosaurs were two to three times the mass of Brachiosaurus, placing them in the same weight class as today’s largest whales. Skeletal mounts of Patagotitan — one of the largest known titanosaurs — are now displayed at the American Museum of Natural History in New York and the Field Museum of Natural History in Chicago. Be sure to visit one of these museums to witness the sheer scale of this incredible dinosaur!

The Relative Bone Strength and Relative Muscle Strength Problem

Horse race – Notice the strain on the horse’s leg.

In the wild, if an animal breaks or fractures a supporting bone, its days are likely numbered. For some large animals, even with good veterinary care, there is often nothing that can be done to save them.

For example, a racehorse can easily shatter a leg just by running. These breaks usually occur in various locations within the lower front leg, though other parts of both the front and rear legs can also be affected. This suggests that such fractures are not due to an inherent weak spot in the leg but rather the simple physics of a heavy animal generating impact forces that exceed the material strength of its bones.

Weighing between 1,800 and 2,000 pounds, Clydesdales are one of the largest horse breeds.

Another indication that these 500-kg animals are approaching a size limitation is the difficulty in treating a shattered leg. Horses have evolved to sleep standing up, an effective survival adaptation that allows them to flee quickly from predators. However, if a horse is forced to bear weight on only three legs for an extended period, the remaining good legs can develop laminitis — a painful and often fatal condition. Soon, standing becomes just as excruciating on these legs as on the originally injured one. Due to these and other complications, euthanasia is often the most humane option.

A leg bone — or any supporting column — can fail in multiple ways, including compression, bending, and twisting. To simplify the discussion, let's focus on compression. A support column will break when the weight applied to it, divided by its cross-sectional area, exceeds the maximum stress the material can withstand. Since stress determines whether a bone will fracture, an animal’s relative bone strength can be defined as its weight divided by the total cross-sectional surface area of the leg bones supporting it.

Bison roaming Yellowstone National Park, Wyoming. Adult male American bison typically weigh between 1,000 and 2,000 pounds.

Larger vertebrates are at a much greater risk of breaking their bones than smaller animals. According to Galileo’s Square-Cube Law, as animals increase in size, their weight (which scales with volume) grows faster than the cross-sectional area of their bones (which scales with surface area). If one animal is twice as large as another in all dimensions, it will weigh eight times as much but have only four times as much cross-sectional bone area. The result? The stress on the larger animal’s bones is twice as high as that of the smaller one. This fundamental scaling principle explains why larger animals have proportionally weaker bones than their smaller counterparts.

To quantify how bone stress increases with size, we can compare the standing stress on the leg bones of various mammals. Using measurements of front and rear leg bone circumferences, we can determine the cross-sectional bone area and calculate the stress experienced by the bones when the animal is merely standing. The table below provides a selection of mammals, ranging from the smallest to the largest, illustrating how bone stress scales with body size.

Stress in the Leg Bones of Mammals while they are Standing

Mammal	Front Leg Circumference (mm)	Rear Leg Circumference (mm)	Approximate Total Bone Area (mm²)	Animal's Weight (N)	Standing Stress (N/M² E5)
Meadow Mouse	5	5	4	0.5	1
Guinea Pig	10	15	29	3.8	1.3
Gray Squirrel	10	13	24	3.9	1.6
Gray Fox	28	26	130	39	3.0
Raccoon	30	28	150	50	3.3
Cloud Leopard	45	41	330	140	4.2
Wolf	62	62	680	470	6.9
Lion	104	94	1700	1400	8.1
Polar Bear	158	135	3820	4390	11.5
Elephant	459	413	33700	57800	17.1

The initial raw data, the front and rear leg circumferences and the mass of each animal is from Anderson, J. F., Hall-Martin, A., and Russell, D. A. 1985. "Long-Bone Circumference and Weight in Mammals, Birds, and Dinosaurs," Journal of Zoology, London (A) 207: 53-61.
Area is calculated as (CF2 + CR2)/2PI, Bone Area = Area * 5/9 to account for hollow center of bones, Standing Stress = Weight / Bone Area

Graph of Standing Stress as a Function of Weight

In comparing mammals while they are just standing, the bones of the larger animals are subjected to greater stress than those of smaller mammals. The larger mammals are at a much greater risk of breaking their bones than the smaller mammals.

The stress on bones increases dramatically when an animal lands after a fall. The force of impact generally depends on both the size of the animal and the height of the fall. A mouse can easily survive a fall from a tall building, but an elephant can be contained with a one-meter (about three-foot) dry moat because falling from even this modest height would likely result in multiple fractures. There is truth to the saying, “The bigger they are, the harder they fall.”

How Muscle Strength Limits the Size of Animals

Just as relative bone strength decreases with size, so does relative muscle strength. The force a muscle can generate is proportional to its cross-sectional area, and so in accordance to Galileo’s Square-Cube Law a larger but similarly shaped animal has proportionally weaker muscles. This explains why small animals, such as house cats, can leap many times their body length, while large animals, such as elephants, struggle to lift themselves off the ground.

Paradoxically, this reduced muscle strength can be an advantage, as it helps limit rambunctious behavior that could lead to a hard landing or an accidental fall, thereby reducing the chance of fracturing bones. For example, while racehorses are bred for speed and often end up breaking their bones, elephants — despite being much larger — usually avoid bone fractures by moving more slowly and never jumping.

To avoid confusion, we need to clarify the difference between absolute and relative strength. Absolute strength can be defined as the total amount of weight an animal can lift, regardless of its own weight. Clearly, larger animals have greater absolute strength than smaller animals. However, when we consider relative strength — the lifting ability of an animal in proportion to its own weight — it is the smallest animals that exhibit the greatest relative strength.

For example, an ant can lift an object fifty times its own weight, a strong person can lift another person, while an Asian elephant can lift only one-fourth of its own weight. The larger, four to seven ton African elephant is not a working animal because its relative strength is even lower.

Whether comparing the muscle strength of different-sized animal species or individuals within a single species, the principle remains the same: relative strength decreases with size. In humans, we can observe this pattern by comparing the relative strength of men of different sizes.

Graph of weightlifting world records for the snatch event as a function of weightlifter's mass

To accurately represent how human strength varies with size, we examine world record data for weightlifting. While most physically fit individuals have the strength to lift another person, what we need to determine is the absolute maximum weight that a large or small human can lift. This information is available in the form of worldwide weightlifting records.

Weightlifters compete only against others of the same size—or more precisely, the same mass. This ensures that, regardless of size, all top athletes have a fair chance to win within their class. By plotting the world records for each weight class, we can observe how the ratio of maximum mass lifted to the lifter’s own mass changes with body size.

World records in the snatch event show that a 56 kg weightlifter lifted a 138 kg mass over his head, demonstrating a relative strength of 2.46, while a much larger 105 kg weightlifter lifted 200 kg, showing a relative strength of 1.90. Besides the snatch event, many other weightlifting events could be used to illustrate this principle. Thus, while the largest weightlifters have the greatest absolute strength, the smallest weightlifters exhibit the greatest relative strength.

For most physically fit human beings we have more than enough relative strength so that getting out of bed in the morning is not outside our physical capacity. But the larger animals that have lower relative strength lifting their body off the ground can be a serious issue. Large farm animals such as cattle or horses exert all the strength that they have when they pick themselves up off the ground. Likewise the large wild animals such as elephants and giraffes need all their strength to perform this task that is not challenging for the smaller animals. As a consequence of these difficulties, it is not surprising that many of these larger animals evolved the behavior of sleeping while standing up.

For most physically fit humans, relative strength is more than sufficient to make getting out of bed in the morning an effortless task. However, for larger animals with lower relative strength, lifting their bodies off the ground can be a serious challenge. Large farm animals such as cattle and horses must exert all their strength to stand up, and similarly, large wild animals like elephants and giraffes need their full strength for this task, which is not difficult for smaller animals. As a consequence of these difficulties, it is not surprising that many large animals evolved the behavior of sleeping while standing up.

Yet numerous dinosaurs were much larger than these animals. Their greater size would mean their relative strength was substantially lower than that of today’s large animals. It is unrealistic to assume that large dinosaurs never fell or otherwise ended up on the ground during their lives. If a Jurassic Park were ever created, any sauropod or other large dinosaur would likely be stuck lying on the ground, much like a helpless whale stranded on a beach.

The Blood Pressure Problem

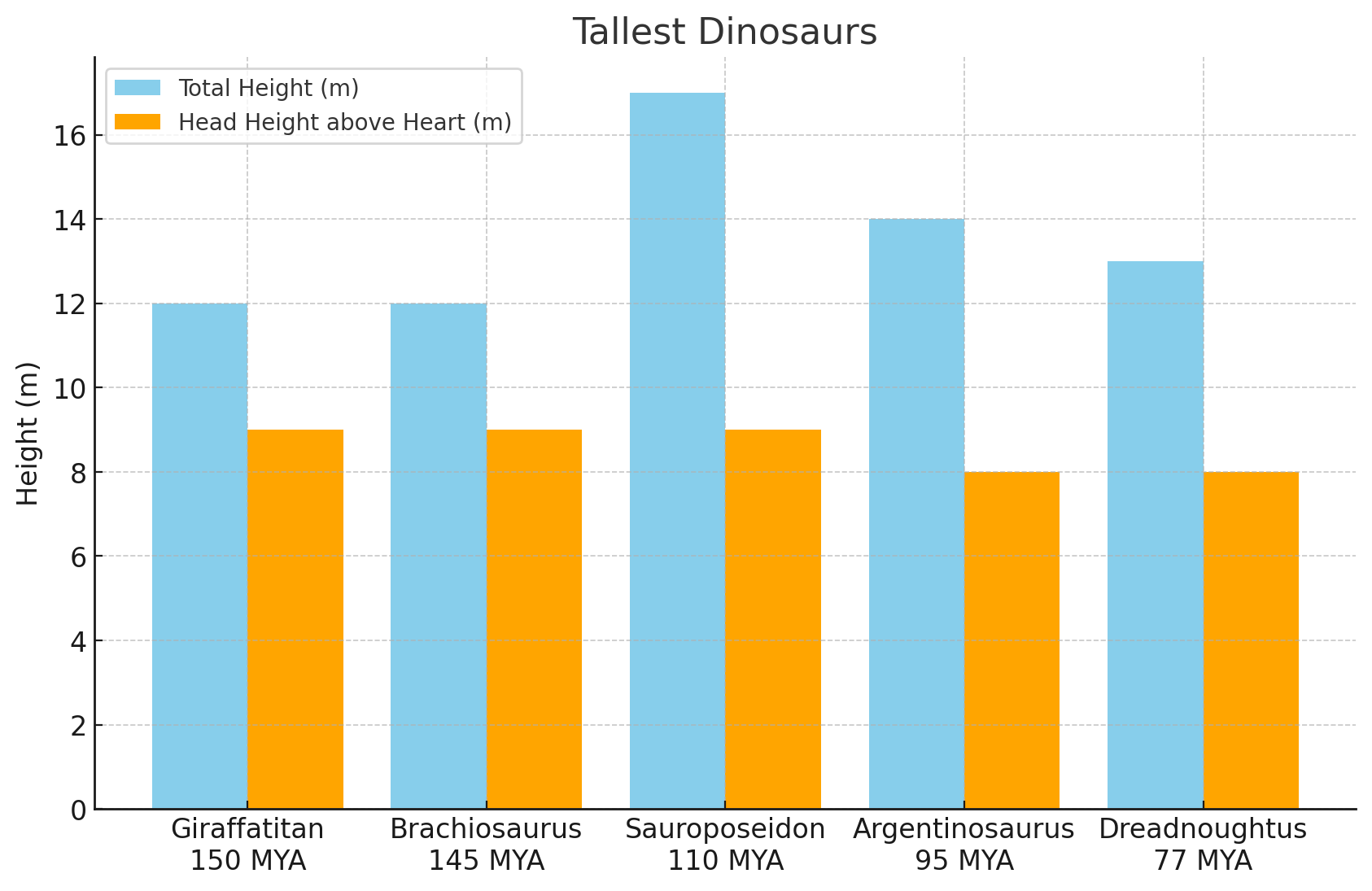
The graph shows that several tall dinosaurs held their heads approximately nine meters above their hearts. Giraffatitan, Brachiosaurus, and Sauroposeidon were giraffe-like sauropods that lived during the late Jurassic and early Cretaceous periods, while Argentinosaurus and Dreadnoughtus were even larger, elephant-like sauropods that lived later in the late Cretaceous. For all of these dinosaurs, paleontologists do not have a scientifically acceptable explanation for how they managed to pump blood up to their heads.

Many researchers have questioned how taller dinosaurs supplied blood to their heads, leading to several highly questionable hypotheses. Some paleontologists suggest that sauropods had an enormous heart capable of generating the necessary pressure. Another theory proposes that they evolved multiple, evenly spaced hearts along their necks to function as a sequential pumping system. More recently, a popular idea suggests that sauropods never raised their heads above their shoulders but instead kept their head low, moving it horizontally while feeding on vegetation.

The variety of hypotheses arises from the challenges of pumping blood to great heights. In a fluid column, pressure increases with depth according to the equation P = ρ g h, where P is pressure, ρ is blood density, g is gravitational acceleration, and h is height. As a result, a pump and its tubing must be strong enough to withstand the high pressure at the base of the column.

A person having their blood pressure taken

Taking Blood Pressure

To understand how blood pressure varies with height, consider how a person's blood pressure is measured. The cuff is placed around the bicep while the person is seated because this aligns the measurement with the heart’s elevation, providing a close approximation of the pressure as blood leaves the heart. If the arm is raised, the reading decreases; if taken at the ankle, it is much higher. This demonstrates how blood pressure depends on height.

Pumping blood to body parts at the same elevation as the heart is relatively easy since the heart only needs to overcome viscous drag in the arteries. In these horizontal circuits, blood pressure remains nearly constant until it reaches the capillaries. This is why a bicep measurement closely reflects the heart’s output pressure.

Arteries and Veins within the Human Body

When we are standing, our blood pressure is much greater at our feet than at our heart or head.

Pumping blood to the lower parts of the body is even easier since gravity assists the downward flow. However, once the blood passes through the capillaries in the feet, it must travel back up to the heart. This is accomplished in part by the pressure exerted by the weight of the blood in the arteries. Valves in the veins also help by relieving pressure in the lower veins between heartbeats. Additionally, these valves allow the leg muscles to act as auxiliary pumps, squeezing blood upward whenever they contract. The discomfort we feel after standing for long periods or sitting during a long plane flight occurs because our leg muscles remain immobile, causing blood to accumulate in the lower veins.

The heart works hardest when elevating blood to the head. With every beat, it must lift all the blood in the vertical column within the arteries leading to the head. We can use the equation P = g ρ h to calculate the required blood pressure P as it leaves the heart to reach a height h, where the brain is located. For an upright adult, the top of the head is about 45 cm above the heart, meaning the minimum pressure needed to reach this height is 35 mm Hg. However, additional pressure is required to push blood through the capillaries. To accomplish both tasks — lifting the blood and pushing it through the capillaries — a normal person requires a blood pressure of about 120/80 mm Hg. The heart's position, closer to the head than the feet, reflects the challenges of pumping blood vertically.

A couple of examples provide further insight into how height affects the cardiovascular system.

Picture of squirrel hanging upside down next to a feeder

Unlike humans, small mammals such as squirrels and bats feel little if any discomfort from being upside down.

Anyone who has attempted a headstand knows it is mildly uncomfortable. In this inverted position, blood pools in the head, causing the face to turn red. However, bats and other small mammals are unaffected by orientation because their bodies are too small to experience significant pressure differences between their highest and lowest points. Only larger, taller terrestrial animals must cope with the challenges of a substantial blood pressure gradient due to elevation.

Another common experience is the dizziness that sometimes occurs when standing up too quickly. While resting horizontally, the heart does not work as hard as it does when standing or exercising. Upon standing, it must suddenly pump much harder to send blood to the brain. If this happens too quickly, blood momentarily fails to reach the brain, temporarily starving brain cells of oxygen and causing a faint or dizzy sensation.

Giraffe reaches up to feed on leaves that other animals cannot reach.

At approximately six feet (or just under 2.0 meters), human beings are relatively tall among most terrestrial vertebrates. However, the giraffe, at 18 feet (or 5.5 meters), is the much taller modern-day champion of height. Our occasional feeling of lightheadedness when standing up is hardly comparable to the 15 feet (or 5.0 meters) elevation change a giraffe experiences when obtaining a drink of water. Without valves in the veins and arteries of its neck, the extreme pressure would cause the blood vessels to rupture when the giraffe lowers its head, and conversely, the giraffe would pass out from lack of blood when it later lifts its head.

Another potential issue is the extreme pressure in the giraffe's lower legs while standing. Anyone who has a job requiring prolonged standing is familiar with the discomfort caused by blood pooling in the lower legs. A giraffe, standing three times taller, faces three times the pressure. Moreover, if its legs were similar to those of other animals, even a small cut on the leg could bleed profusely and potentially be life-threatening.

To prevent blood from pooling in its lower legs, the giraffe's legs are surrounded by tough, thick skin that counteracts the blood pressure. Inside the skin, there is a thick layer of fibrous tissue, and the leg's blood vessels are located deep within to avoid the potentially lethal problem of bleeding from a cut.

Yet, the giraffe's greatest cardiovascular challenge is having a strong enough heart to pump blood to its brain. To produce the necessary blood pressure, the giraffe's heart is a massive muscle with walls up to three inches (eight cm) thick, weighing 25 pounds (11 kg). Even more impressive is that the giraffe's resting heart rate is 65 beats per minute—about twice what is expected for an animal of its size. The giraffe's powerful, 'revved-up' heart produces a blood pressure of 300/180 mm Hg, necessary for the blood to reach its head. Giraffes have a relatively short lifespan of only 20 years and are prone to heart attacks as a result of these cardiovascular adaptations.

Yet, if the giraffe is an amazing example of overcoming cardiovascular challenges to achieve its height, what should we think of the Brachiosaurus, which stood at a height of 13 meters? While the giraffe's head is 2.5 to 3.0 meters above its heart, the Brachiosaurus' head was about 9.0 meters above its heart. As the variety of unlikely proposals shows, paleontologists are baffled by this problem.

The sauropod blood pressure paradox has been debated for several years and is now even appearing in physics textbooks. Increasingly, paleontologists are coming to believe that the Brachiosaurus could not have held its head up. Likewise, Apatosaurus and other sauropods could not have reared up on their hind legs to reach higher foliage.

Yet remounting all the Brachiosaurus exhibits to lower the head is not the solution. This ad hoc solution does not explain why the Brachiosaurus has a posture suited for reaching up high. The Brachiosaurus, the "arm lizard," and its cousins are the only dinosaurs with longer front legs than rear legs. The logical explanation for these longer front legs is that the combination of the longer legs and its long neck serve the purpose of extending the Brachiosaurus' reach to the highest foliage. Thus, we face the paradox of an animal that is built for its head and mouth to reach maximum height, yet at this great height, its heart lacks the ability to pump blood up to its head.

The paradox of how the giant pterosaurs flew is the subject of the next chapter.

| Previous Chapter | Return to Home Page | Next Chapter |

2. The Paradox of Large Dinosaurs and Flying Pterosaurs